What is Projectile Motion – Explained

Projectile Motion

” Projectile motion is the two-dimensional motion under constant acceleration due to gravity.”

Projectile motion is a form of movement experienced by an object or particle that is forecasted near the Earth’s surface and moves along a curved path under the action of gravity only. This curved path was revealed by Galileo to be a parabola, however may also be a line in the special case when it is thrown straight upwards.

Description

Let us think about the motion of a ball when it is thrown horizontally from a certain height. It is observed that the ball travels forward along with falls downwards; until it strikes something. Suppose that the ball leaves the hand of the thrower at point A. Let this speed be v_x. According to Newton’s first law of motion, there will be no velocity in the horizontal direction, unless a horizontally directed force acts on the ball. Overlooking the air friction, just force acting on the ball throughout the flight is the force of gravity.

There is no horizontal force acting on it. So, its horizontal speed will remain unchanged and will be v_x, up until the ball hits something. The horizontal movement of the ball is simple. The ball moves with a consistent horizontal velocity component. Hence horizontal distance x is given by

x = v_x x t

The vertical motion of the ball is also not complicated. It will accelerate downward under the force of gravity and hence a = g. This vertical motion is the same when it comes to a freely falling body. Because initial vertical velocity is zero, for this reason, vertical distance y, is provided as

 

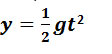
Projectiles

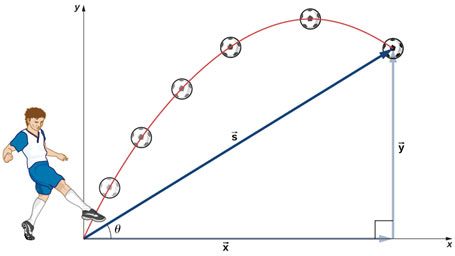
lt is not essential that an object must be thrown with some initial velocity in the horizontal direction. A football kicked off by a player; a ball thrown by a cricketer and a missile fired from a launching pad, all projected at some angles with the horizontal, are called projectiles.

In such cases, the motion of a projectile can be studied quickly by resolving it into horizontal and vertical components that are independent of each other.
Suppose that a projectile is fired in a direction angle θ with the horizontal by velocity v_i. Let components of velocity v_i along the horizontal and vertical directions be v_i cos θ and v_i sin θ respectively.

The horizontal acceleration is a_x = 0 due to the fact that we have actually neglected air resistance and no other force is acting along this direction whereas vertical velocity a_y = g. Thus, the horizontal component v_ix remains continuous and at any time t, we have:

v _{f x} = v_ix = v_i cos θ

Now we think about the vertical motion. The initial vertical component of the speed is v_i sin θin the upward direction. Using the vertical component V_fy of the velocity at any instant t is given by

v _{f y} = v_i sin θ – g t

The magnitude of velocity at any instant is

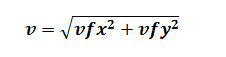
The angle ϕ which this resultant velocity makes with the horizontal can be found from

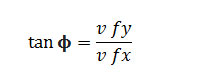
In projectile motion one may want to figure out the height to which the projectile rises, the time of flight, and horizontal range. These are described below.

Height of the Projectile
In order to determine the maximum height of the projectile attains, we use the equation of motion

2 a S = v_f² – v_i²

As the body moves upward, so a = – g, the initial vertical speed v_iy, = v_i sin θand V_fy = 0 due to the fact that the body comes to rest after reaching the highest point. Since

S= height= h
-2 g h = 0 – v_i²sin² θ

 

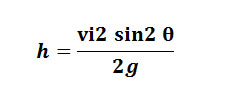
Time of Flight

The time taken by the body to cover the distance from the place of its projection to the place where it strikes the ground at the same level is called the time of flight.

This can be acquired by taking S = h = 0, since the body goes up and comes back to the same level, hence covering no vertical distance. If the body is projecting with velocity v making angle θ with a horizontal, then its vertical component will be v_i sin θ. For this reason, the equation is.

S = v_i t + ½ g t²
0 = v_i sin θ t –½ g t²
t= 2v_i sin θ/ g

 

where t is the time of flight of the projectile when it is projected from the ground.

Range of the Projectile

The optimum distance which a projectile cover in, the horizontal direction is called the range of the projectile. To determine the range R of the projectile, we multiply the horizontal component of the velocity of projection with the overall time taken by the body after leaving the point of projection.
Thus:

R =v_ix x t

R =v_i cos θ x2v_i sin θ/ g

R =v_i²2sin θcos θ/g

But, 2sin θcos θ, thus the range of the projectile depends upon the velocity of projection and the angle of projection.

For that reason,

R =v_i²sin2 θ/g

For the variety R to be optimal, the element sin2 θ must have a maximum value which is 1 when 2 θ= 90 ° or θ = 45 °.

Summary

The projectile motion is the motion of constant acceleration due to gravity. The path in that is the trajectory and the object that is projected called projectile.

The projectile motion describes the scenario that the constant acceleration which is necessarily unidirectional can produce two-dimensional motion.

According to Newton’s first law of motion, there is no velocity in a horizontal direction and overlooking the air friction the projectile only experiences the force of gravity. So, its speed will remain unchanged.

For the study of projectile motion, it is resolved into horizontal and vertical components. The projectile motion has the shape of parabola revealed by Galileo, in curved path, is the characteristic of this motion.