What is the Equation?
An equation is a mathematical statement that two things are equal. It consists of two expressions, one on each side of an ‘equals’ sign
For Example:
8 + 2 = 10
This equation states that 10 is equal to the sum of 8 and 2, which is for sure, true. In an equation, the left-hand side is always equal to the right-hand side.
Equations containing Variables
The most usual equations consist of one or more variables. If we suppose x stands for an unknown number and write down the equation as:
X=11+4
As we know, the left hand side and right hand side of equations are equal, so we can say that x must be 11+4 or 15. This is the only answer that x can have or that makes the equation a true statement. We can say that x=15 ‘satisfies’ the above equation.
The process of calculating the values for the unknowns is known as “solving the equations”. We usually say that we “solve for value of x” – means solving the equations to find the value of the unknown value x.
A habitual mistake
You usually look at things that are called as equations but actually, they are not the equations.
For example:
You can see something like this and referred to as an equation:
X3−2x2+4
This statement does not have an equal sign in it, and that is why this is not an equation. This statement is called as an ‘expression’.
Algebraic Equations
Equations often contain algebra. Algebra is used in maths when you do not know the exact number in a calculation.
These are the combination of polynomials, equal sign, and constant values.
For Example:
4x2 + 5x + 2 = 0
Different types of equations in mathematics
Following are the types of equations on the basis of the power of variables
Linear equations
Linear means having one line. In these equations, the highest degree of the variable is 1. These are equations of the type
E= ax+b
where ‘a’ and ‘b’ are real numbers and ‘x’ is a variable that cannot be equal to zero. In this equation, ‘x’ has exponent equal to 1.
Example
E= 5x+6, E= x+4
These are linear equations.
Quadratic equations
These are the equations that contain maximum power or exponent of variable equals to 2. These are the equations of the type
ax2+bx+c= 0
where ‘a’ and ‘b’ are real numbers and ‘x’ is a variable that cannot be equal to zero.
Example:
4x2 + 5x + 6 = 0
3x2 + 2x + 8 = 0
These are quadratic equations.
Radical equations
These are equations whose maximum power on the variable is 1/2 and have more than one term. Here we use the radical symbol and the variable is lying inside a radical symbol usually we say that in a square root.
Example:
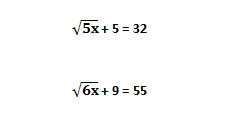
These are radical equations.
Polynomial equations
A polynomial equation is the one that takes away the limit of the highest exponent of variables. The equation consists of several terms and raised to any power of the variable.
Example:
4x5 + 3x3 + 6x2 + 8x + 15 9x9 + 8x7 + x3 + 4x + 20
These are the polynomial Equations.
Some other types of Equations
Exponential equations
These are the equations that contain variables in the place of exponents.
Example:
45x = 5
2y = 10
These are Exponential Equations.
Trigonometric equations
These are equations in which the variables are affected by trigonometric functions.
cosx + 1 = + 5 tanx + 10 = 15
These are the trigonometric Equations.
Uses of Equations in real life
Many professionals use equations every day, including air traffic controllers, architects, computer programmers, and carpenters. Engineers, architects, and video-game designers all use equations in their work too.

