What is Simple Harmonic Motion?
Simple Harmonic Motion or SHM is defined as a motion in which the restoring force is directly proportional to the displacement of the body from its mean position. The direction of this restoring force is always towards the mean position. The velocity of a particle executing simple harmonic motion is given by,
a (t) = -ω2 x(t)
Here, ω is the angular velocity of the object.
Simple harmonic motion can be referred to as an oscillatory motion in which the velocity of the particle at any position is directly proportional to the displacement from the mean position. It is a special case of oscillatory motion.
All the Simple Harmonic Motions are oscillatory and also periodic but not all oscillatory motions are SHM. Oscillatory motion is likewise called the harmonic motion of all the oscillatory motions wherein the most important one is simple harmonic motion (SHM).
Mass-Spring System
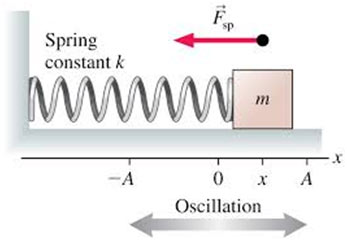
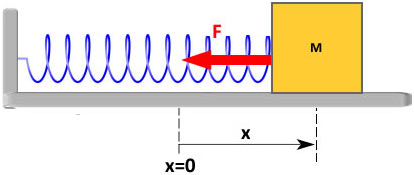
Among the simplest kinds of oscillatory motion is that of a horizontal mass-spring system. If the spring is stretched or compressed through a little displacement x from its mean position, it applies a force F on the mass. According to Hooke’s law, this force is directly proportional to the change in length x of the spring i.e.,
F = – k x
where x is the displacement of the mass from its mean position O, and k is a constant called the spring constant defined as
k = – F/ x
The value of k is a measure of the stiffness of the spring. Stiff springs have a large value of k and soft springs have a small value of k.
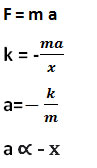
It implies that the acceleration of a mass attached to a spring is directly proportional to its displacement from the mean position. Hence, the horizontal motion of a mass-spring system is an example of simple harmonic motion.
The negative sign indicates that the force applied by the spring is always directed opposite to the displacement of the mass. Since the spring force constantly acts towards the mean position, it is sometimes called a restoring force.
A restoring force constantly pushes or pulls the item performing oscillatory motion towards the mean position. Initially, the mass m is at rest in position mean O and the resultant force on the mass is zero. Suppose the mass is pulled through a distance x up to extreme position A and after that released.
The restoring force exerted by the spring on the mass will pull it towards the mean position O. Due to the restoring force the mass returns, towards the mean position O. The magnitude of the restoring force reduces with the distance from the mean position and becomes zero at O.
Nevertheless, the mass gains speed as it moves towards the mean position and its speed ends up being optimum at O. Due to inertia the mass does not stop at the mean position O but continues its motion and reaches the extreme position B.
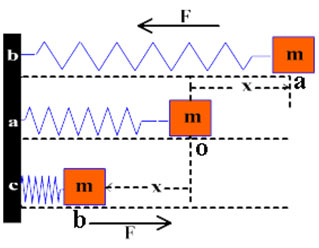
As the mass moves from the mean position O to the extreme position B, the restoring force acting on it towards the mean position steadily increases in strength. Thus, the speed of the mass reduces as it moves towards the extreme position B. The mass finally comes briefly to rest at the extreme position B. Ultimately the mass returns to the mean position due to the restoring force.
This procedure is repeated, and the mass continues to oscillate backward and forward about the mean position O. Such motion of a mass attached to a spring on a horizontal frictionless surface area is referred to as Simple Harmonic Motion (SHM). The time duration T of the simple harmonic motion of a mass ‘m’ connected to spring is given by the below formula:
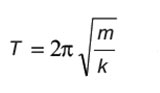
Essential features of SHM are summarized as:
- A body carrying out SHM always vibrates about a fixed position.
- Its acceleration is always directed towards the mean position.
- 4. The magnitude of velocity is always directly proportional to its displacement from the mean position i.e., acceleration will be zero at the mean position while it will be optimal at the extreme positions.
- Its velocity is optimum at the mean position and zeroes at the extreme positions.
Now we discuss various terms that characterize simple harmonic motion.
- Vibration: One complete round trip of a vibrating body about its mean position is called one vibration.
- Time Period (T): The time taken by a vibrating body to finish one vibration is called the time period.
- Frequency (f): The number of vibrations or cycles of a vibrating body in one second is called its frequency. It is reciprocal of time period i.e., f = 1/T.
- Amplitude (A): The optimum displacement of a vibrating body on either side from its mean position is called its amplitude.
MCQs:
- What is Simple Harmonic Motion (SHM)?
- A) Motion in which the restoring force is inversely proportional to displacement
- B) Motion in which the restoring force is directly proportional to displacement
- C) Motion in which the restoring force is independent of displacement
- D) Motion in which the restoring force is constant
- Answer: B) Motion in which the restoring force is directly proportional to displacement
- What is the equation representing the velocity of a particle in simple harmonic motion?
- A) v(t) = ω^2 x(t)
- B) v(t) = -ω x(t)
- C) v(t) = -ω^2 x(t)
- D) v(t) = ω x(t)
- Answer: B) v(t) = -ω x(t)
- What is the angular velocity (ω) in simple harmonic motion?
- A) The rate of change of displacement
- B) The rate of change of velocity
- C) The rate of change of acceleration
- D) The rate of change of frequency
- Answer: A) The rate of change of displacement
- According to Hooke’s law, what is the relationship between the force applied by a spring (F) and the displacement (x)?
- A) F = k / x
- B) F = k * x
- C) F = -k * x
- D) F = -k / x
- Answer: C) F = -k * x
- What does the constant ‘k’ represent in Hooke’s law?
- A) Mass of the object
- B) Stiffness of the spring
- C) Time period of oscillation
- D) Amplitude of the motion
- Answer: B) Stiffness of the spring
- What term characterizes the motion of a mass-spring system on a horizontal frictionless surface?
- A) Simple Harmonic Motion (SHM)
- B) Uniform Circular Motion (UCM)
- C) Linear Motion
- D) Random Motion
- Answer: A) Simple Harmonic Motion (SHM)
- What is the direction of the restoring force in simple harmonic motion?
- A) Opposite to the displacement
- B) Same as the displacement
- C) Perpendicular to the displacement
- D) Independent of the displacement
- Answer: A) Opposite to the displacement
- What happens to the speed of the mass as it moves towards the mean position in SHM?
- A) Increases
- B) Decreases
- C) Remains constant
- D) Becomes zero
- Answer: B) Decreases
- What term describes one complete round trip of a vibrating body about its mean position?
- A) Amplitude
- B) Time period
- C) Frequency
- D) Vibration
- Answer: D) Vibration
- How is frequency related to the time period in simple harmonic motion?
- A) f = T
- B) f = 1/T
- C) f = T/2
- D) f = 2T
- Answer: B) f = 1/T
- What is the meaning of amplitude in simple harmonic motion?
- A) The time taken for one vibration
- B) The number of vibrations per second
- C) The maximum displacement from the mean position
- D) The stiffness of the spring
- Answer: C) The maximum displacement from the mean position
- Which of the following statements about SHM is correct?
- A) Acceleration is zero at all positions
- B) Velocity is zero at all positions
- C) Velocity is maximum at the mean position
- D) Acceleration is maximum at the extreme positions
- Answer: D) Acceleration is maximum at the extreme positions
- What is the direction of acceleration in SHM?
- A) Towards the mean position
- B) Opposite to the displacement
- C) Perpendicular to the velocity
- D) Along the displacement
- Answer: A) Towards the mean position
- How is the time period (T) of SHM related to the frequency (f)?
- A) T = f
- B) T = 1/f
- C) T = f/2
- D) T = 2f
- Answer: B) T = 1/f
- Which of the following motions is an example of simple harmonic motion?
- A) Projectile motion
- B) Circular motion
- C) Pendulum motion
- D) Motion along a straight line with constant velocity
- Answer: C) Pendulum motion
- What happens to the restoring force as the mass moves towards the mean position in SHM?
- A) Increases
- B) Decreases
- C) Remains constant
- D) Becomes zero
- Answer: A) Increases
- What is the magnitude of velocity at the mean position in SHM?
- A) Zero
- B) Maximum
- C) Minimum
- D) Constant
- Answer: B) Maximum
- What is the relationship between the displacement and the acceleration in SHM?
- A) Directly proportional
- B) Inversely proportional
- C) No relationship
- D) Exponential relationship
- Answer: A) Directly proportional
- What happens to the velocity as the mass moves towards the extreme positions in SHM?
- A) Increases
- B) Decreases
- C) Remains constant
- D) Becomes zero
- Answer: B) Decreases
- What is the direction of the velocity at the extreme positions in SHM?
- A) Towards the mean position
- B) Opposite to the displacement
- C) Perpendicular to the acceleration
- D) Along the displacement
- Answer: D) Along the displacement
- Which equation represents the displacement of a particle in SHM?
- A) x(t) = ω^2 v(t)
- B) x(t) = -ω v(t)
- C) x(t) = -ω^2 v(t)
- D) x(t) = ω v(t)
- Answer: D) x(t) = ω v(t)
- What term describes the stiffness of the spring in SHM?
- A) Mass
- B) Time period
- C) Amplitude
- D) Spring constant
- Answer: D) Spring constant
- What is the essential feature of SHM regarding acceleration?
- A) Always directed towards the mean position
- B) Always directed away from the mean position
- C) Zero at all positions
- D) Maximum at all positions
- Answer: A) Always directed towards the mean position
- What characteristic distinguishes SHM from other oscillatory motions?
- A) Time period
- B) Amplitude
- C) Restoring force proportional to displacement
- D) Frequency
- Answer: C) Restoring force proportional to displacement
Wrap up
In summary, Simple Harmonic Motion (SHM) is a type of oscillatory motion characterized by a restoring force that is directly proportional to the displacement of an object from its mean position. This motion is exemplified by the behavior of systems such as mass-spring systems, where a mass attached to a spring undergoes periodic motion.
Key points regarding SHM include:
- The acceleration of an object undergoing SHM is always directed towards the mean position.
- The velocity of the object is directly proportional to its displacement from the mean position, with maximum velocity at the mean position and zero velocity at the extreme positions.
- Essential terms describing SHM include vibration (one complete round trip of a vibrating body), time period (the duration for one vibration), frequency (the number of vibrations per second), and amplitude (the maximum displacement from the mean position).
Overall, SHM exhibits regular, repetitive motion and is fundamental to understanding various physical phenomena, from pendulum oscillations to wave behavior.