An Introduction to Quantum Numbers
The set of numbers used to explain the position as well as the energy of the electron in an atom are called quantum numbers. These explain the movement and trajectories of each electron within an atom. Quantum numbers are the sets of mathematical values that give the appropriate solutions to the Schrodinger wave formula for the hydrogen atom.
An electron in an atom is entirely described by its four quantum numbers. You understand that a complete address of a person comprises his name, the city in which he lives, the block, the road, and also that’s personal home number. On similar grounds, quantum numbers work as identification numbers or labels, which totally describe an electron. These quantum numbers specify the position of an electron in an atom.
The Four Quantum Numbers
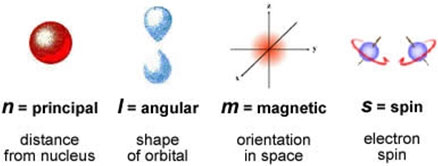
There are 4 quantum numbers that can describe the electron completely.
- Principal quantum number (n)
- Azimuthal quantum number (ℓ)
- Magnetic quantum number (m)
- Spin quantum number (s)
All quantum numbers are defined and listed below in this post.
Principal Quantum Number (n)
The different energy levels in Bohr’s atom are represented by ‘n’. This is called the primary quantum number by Schrodinger. Its values are non-zero, positive integers up to infinity.
n = 1, 2, 3, 4, 5, … … … …
The value of n represents the shell or energy level in which the electron moves around the nucleus. Letter symbols K, L, M, N, and so on are likewise used to represent the different shells. For example, when n =1, it is called K shell, for n = 2, it is L shell, and so forth.
The values of n additionally establish the location of an electron in an atom, i.e., the distance of the electron from the nucleus, the greater the value of ‘n’ better will certainly be the range of electron from the core. It is a quantitative measure of the dimension of an electronic shell, ‘n’ likewise offers us the energy of electron in a shell. Bohr’s results aid us to recognize the relationships between the distance and energy of electrons.
Azimuthal Quantum Number (ℓ)
It has actually currently been stated in the issues of Bohr’s version that a spectrometer of high resolving power shows that an individual line in the range is more split into several extremely fine lines. This point can be discussed by saying that each shell is separated right into subshells. So, just the primary quantum number (n) is not sufficient to discuss the line range. There is one more subsidiary quantum number called the azimuthal quantum number which is used to represent the subshells. The values of azimuthal quantum number (ℓ).
(ℓ) = 0, 1, 2, 3, … … … … … … … … … … … (n-1)
These values represent different subshells, which are assigned by small letters, s, p, d, f. They mean sharp, primary, diffused, and fundamental, respectively. These are the spectral terms utilized to describe the series of lines observed in the atomic spectrum. The values of azimuthal quantum numbers always start from zero.
A subshell might have different shapes relying on the value of (ℓ). It may be round, dumbbell, or a few other complex shapes. The value of ‘ℓ’ is related to the form of the subshell as adheres to:
| ℓ | s-subshell | spherical | |
| ℓ | 1 | p-subshell | dumb-bell |
| ℓ | 2 | d-subshell | complicated form |
The Magnetic Quantum Number (m)
The magnetic quantum number ml determines the variety of orbitals and also their alignment within a subshell. Consequently, its value depends on the orbital angular momentum quantum number l. Offered a specific l, ml is an interval varying from– l to +l, so it can be zero, an unfavorable integer, or a positive integer.
m = 0, ± 1, ± 2, ± 3, … … … ……
Spin Quantum Number (s)
Alkali metals have one electron in their outer shell. We can record their emission spectra when the outermost electron leaps from an excited state to a ground state. When the spectra are observed using a high settling power spectrometer, each line in the spectrum is found to contain pair of lines, this is called a doublet line framework.
We need to keep in mind, that the doublet line framework is different from the fine spectrum of hydrogen.
In 1925, Goudsmit and Uhlenbech suggested that an electron while moving in an orbital around the nucleus likewise rotates or spins concerning its own axis either in a clockwise or anti-clockwise direction.
This is additionally called self-rotation. This spinning electron is related to a magnetic field and therefore a magnetic moment. Hence, opposite magnetic fields are produced by the clockwise and anti-clockwise rotates of electrons. This spin activity is in charge of the doublet line structure in the spectrum.