Quadratic Equation and Quadratic formula

Quadratic Equation

A quadratic equation is a second-order polynomial equation in a single variable x.

The name Quadratic originates from “quad” denoting square because the variable gets squared (like x²).

It is likewise called an “Equation of Degree 2” (because of the “2” on the x).

Standard Notation

ax² + bx + c = 0

with a=0. Since it is a second-ordered polynomial equation, the basic theorems of algebra ensure that it has two answers. These answers might be both real, or both complex.

An example of the Quadratic Equation

6x² – 3x + 1 = 0

 

4x² + 1 = 0 (lacking linear coefficient or ‘bx’)

 

2x² – 10x = 0 (lacking constant or ‘c’)

Messed up Quadratic Equation

As we learned formerly, the Standard Notation of a Quadratic Equation is

ax² + bx + c = 0

However, in some cases, a quadratic equation doesn’t appear like that!

Example

 

4x = 3x² + 2

 

It can be sorted in the standard notation as:

3x² – 4x + 2 = 0

 

It is done by moving the linear coefficient on the other side of equality.

 

x (x + 1) = 3

First of all, multiply ‘x’ with the term ‘(x + 1)’ as:

 

x² + x = 3

 

now move ‘3’ on the other side of equality as:

 

x² + x – 3 = 0

 

Solving the Quadratic Equation

The “solutions” to the Quadratic Equation are where it is equal to zero.

 

They are also called “roots“, or in some cases “zeros“. There are generally 2 solutions.

 

Typically, the most basic way to solve “ax² + bx + c = 0” for the value of x is to factor the quadratic equation, set each factor equal to zero, and then solve each factor.

Example

4x² – 4x = 0

4x (x – 1) = 0

Now,

4x = 0 or x – 1 = 0

x = 0 or x = 1

x = {0,1}

Another Example:

x² + 6x + 8 = 0

x² + 4x + 2x + 8 = 0

x (x+4) + 2 (x+4) = 0

(x+4) (x+2) = 0

 

Now,

x + 4 = 0 or x + 2 = 0

x = -4 or x = -2

 

x = {-2, -4}

However, in some cases, the quadratic is too disordered, or it does not factor at all, or you just do not feel like factoring. While factoring may not always be successful, the Quadratic Formula can always find the solution.

what is the Quadratic Formula?

The Quadratic Formula utilizes the “a”, “b”, and “c” from “ax² + bx + c”, where “a”, “b”, and “c” are simply numbers; they are the “numerical coefficients” of the quadratic equation they have actually given you to solve.

The roots x can be identified by completing the square,

 

The above-proved equation     is known as the quadratic formula. The +- sign in the equation shows that there are two roots one with the positive sign and the other with the negative sign. By taking the square root, it is known that the result is either positive or negative as squaring a positive or negative number is the same.

Who invented the Quadratic Formula? The very first simple mathematical try to come up with a quadratic formula was done by Pythagoras in 500 BC. Euclid did the very same thing in Alexandria, Egypt. Euclid used a simple geometric method. And he created a general formula to solve the equation.

Following is the example related to solve a Quadratic Equation with the help of Quadratic Formula:

x² + 6x + 8 = 0

We have

a = 1, b = 6, c = 8.

Now, put these values in the formula .

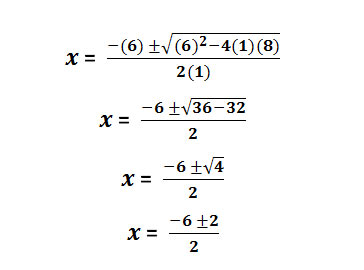
Now, 

{-4, -2}