Hardy-Weinberg Theorem
Hardy-Weinberg theorem is an algebraic formula that describes the hereditary equilibrium within a population.
Hardy-Weinberg theorem is named for the two scientists Wilhelm Weinberg, a German physician, and Godfrey Harold Hardy, a British mathematician, who derived the principle independently in 1908.
Population, Gene Pool, Allele and Genotype Frequencies
A population is a localized group of individuals belonging to the same species. For now, we will define a species as a group of populations that have the possibility to interbreed in nature. Each species has a geographical variety within which individuals are not expanded evenly, but are usually concentrated in several localized populations.
A population may be isolated from others of the same species, exchanging genetic products just seldom. Such isolation is especially typical for populations confined to widely separated islands, unconnected lakes, or mountain ranges separated by lowlands. Within a population, individuals are concentrated in centers and are more likely to interbreed with members of the same population than with members of other populations.
For that reason, individuals near a population center are, on average, more closely related to one another than to members of other populations.
The total aggregate of genes in a population at any one time is called the population’s gene pool. It includes all alleles at all gene loci in all individuals of the population. For a diploid species, each locus is represented twice in the genome of an individual, who might be either homozygous or heterozygous.
If all members of a population are homozygous for the same allele, that allele is stated to be fixed in the gene pool. More frequently, there are two or more alleles for a gene, each having a relative frequency (percentage) in the gene pool.
Let us consider an example.
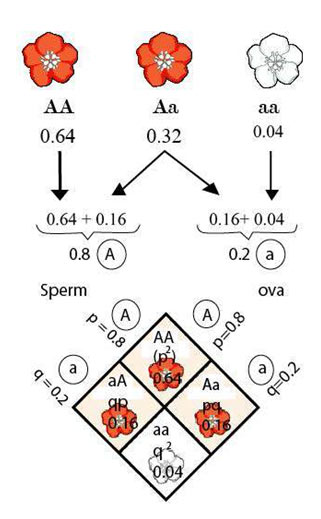
Imagine a wildflower population with 2 varieties contrasting in flower color. An allele for pink flowers, which we will symbolize by A, is entirely dominant over an allele for white flowers, represented by a. Suppose these are the only two alleles for this locus in the population. Our imaginary population has 500 plants.
Twenty have white flowers since they are homozygous for the recessive allele; their genotype is aa. Of the 480 plants with pink flowers, 320 are homozygous (AA) and 160 are heterozygous (Aa). Since these are diploid organisms, there is an overall of 1000 copies of genes for flower color in the population.
The dominant allele represents 800 of these genes (320×2 = 640 for AA plants, plus 160×1 = 160 for an individuals). Therefore, the frequency of the A allele in the gene pool of this population is80%, or 0.8.
And since there are only two allelic kinds of the gene, the allele must have a frequency of 20%, or 0.2. Related to these allele frequencies are the frequencies of genotypes. In our model wildflower population, these frequencies are:
AA= 0.64 (64%) (320 out of 500 plants),
Aa= 0.32 (160/500) and
aa = 0.04 (20/500).
Hardy-Weinberg Theorem
The frequencies of genotypes of non-evolving populations are explained by Hardy- Weinberg theorem.
“It states that the frequencies of alleles and genotypes in a population’s gene pool remain constant over the generations unless acted upon by agents other than sexual recombination. So, shuffling of alleles due to meiosis and random fertilization has no effect on the overall genetic structure of a population.”
A general equation called the Hardy- Weinberg equation is used for computing the frequencies of alleles and genotypes in populations at equilibrium.
Estimations of Allelic Frequency
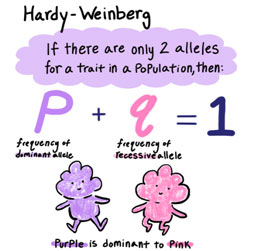
For a gene locus where only 2 alleles occur in a population, population geneticists use the letter P to represent the frequency of one allele and the letter q to represent the frequency of the other allele.
- P = Dominant allele
- q= Recessive allele
In the imaginary wild flower population, P= 0.8 and q= 0.2.
Note that P+ q= 1;
- The combined frequencies of all possible alleles must account for 100% of the genes for that locus in the population.
- If there are just 2 alleles and we understand the frequency of one, the frequency of others can be calculated:
if P + q = 1, then 1 – P = q or 1 – q + P.
Estimation of Gene frequency
When gametes combine their alleles to form zygotes, the probability of producing an AA genotype is P2. In the wildflower population, P-0.8, and P2= 0.64, the probability of an A sperm fertilizing an A ovum to produce an AA zygote.
The frequency of individuals homozygous for the other allele aa is q2, or 0.2 x0.2= 0.04 for the wildflower population. There are two ways in which an Aa genotype can arise, depending upon which parent contributes the dominant allele. For that reason, the frequency of heterozygous individuals in the population is 2Pq (2×0.8 x0.2= 0.32, in our example). If we have actually calculated the frequencies of all possible genotypes properly, they ought to amount to 1:
P2 + 2pq + q2 = 1
Frequency of AA Frequency of Aa Frequency of aa
For our wildflowers, this is.
0.64 + 0.32 + 0.04 =1
In fact, the Hardy-Weinbergtheorem is a binomial expansion.
(P+ q) 2 = P2 + 2Pq + q2
Factors affecting Gene Frequency
Lots of factors can change gene frequency. Out of these five affect the proportion of homozygotes and heterozygotes enough to produce significant variances from the percentage claimed by the Hardy Weinberg principle. They are as follows.
1.Mutations
The ultimate source of all modifications and changes; individual mutations occur so hardly ever that mutation alone does not change allele frequency much.
2.Migration
A really powerful representative of change, migration locally acts to prevent evolutionary changes by avoiding populations that exchange members from diverging from one another. Emigration and migration of members of a population, cause disruption in the gene pool.
3.Genetic drift
It is the change in frequency of alleles at a locus that happens by chance. In small populations, such fluctuations may lead to the loss of particular alleles. This may happen in a little population when a few individuals fail to reproduce and after that genes are lost from the population.
4.Non-random mating
Inbreeding is the most typical kind; it does not alter allele frequency, however, reduces the percentage of heterozygous individuals. Individuals with particular genotypes often mate with one another more commonly than would be anticipated on a random basis. This is called non-random mating, causing the frequencies of specific genotypes to differ significantly from those forecasted by the Hardy- Weinberg principle.
5.Selection
Some individuals leave behind more offspring than others, and the rate at which they do so is affected by their acquired qualities. This is called selection. Selection can be an artificial selection or natural selection. In artificial selection, the breeders pick for the wanted characters. In natural selection, the environment plays this function, thus affecting the proportions of genes in a population.
Summary
Evolution is central to biology and is not a creative work force. It is not working for the progress. Sometimes, its rate is slow and sometimes it is rapid. But there are some conditions in which evolution does not occur at all.
The theories of population genetics explain how evolution can occur, progress or stopped. The Hardy-Weinberg theorem is one that explains what happens to the frequency of alleles in a population over time.
It states that if certain assumptions are met, evolution will not occur because the allelic frequencies will not change from generation to generation, even though the specific mixing of alleles in individuals may vary. Hardy – Weinberg theorem provides a useful theoretical framework.
Multiple Choice Questions (MCQs):
- What is the Hardy-Weinberg theorem?
- a) A biological principle governing gene expression
- b) An algebraic formula describing hereditary equilibrium
- c) A theorem for calculating mutation rates
- d) A rule for population migration
Answer: b) An algebraic formula describing hereditary equilibrium
- Who are the scientists credited with the Hardy-Weinberg theorem?
- a) Wilhelm Weinberg and Charles Darwin
- b) Gregor Mendel and Godfrey Harold Hardy
- c) Wilhelm Weinberg and Godfrey Harold Hardy
- d) Charles Darwin and Alfred Russel Wallace
Answer: c) Wilhelm Weinberg and Godfrey Harold Hardy
- What does the Hardy-Weinberg theorem state about allele and genotype frequencies in a population?
- a) They remain constant over generations unless acted upon by factors other than sexual recombination.
- b) They change randomly with each generation.
- c) They are solely influenced by migration.
- d) They are independent of the gene pool.
Answer: a) They remain constant over generations unless acted upon by factors other than sexual recombination.
- What is the total aggregate of genes in a population at any one time called?
- a) Genetic diversity
- b) Gene assortment
- c) Gene pool
- d) Genetic equilibrium
Answer: c) Gene pool
- If P represents the frequency of the dominant allele, what does q represent?
- a) Recessive allele frequency
- b) Homozygous allele frequency
- c) Heterozygous allele frequency
- d) Dominant allele frequency
Answer: a) Recessive allele frequency
- In the Hardy-Weinberg equation, if P + q = 1, what does 1 – P equal?
- a) Dominant allele frequency
- b) Recessive allele frequency
- c) Heterozygous allele frequency
- d) Homozygous allele frequency
Answer: b) Recessive allele frequency
- What is the probability of producing an AA genotype when gametes combine their alleles to form zygotes?
- a) P2
- b) q2
- c) 2Pq
- d) P + q
Answer: a) P2
- How is migration likely to affect the Hardy-Weinberg equilibrium?
- a) Enhances divergence between populations
- b) Acts as a stabilizing factor
- c) Causes random fluctuations in allele frequencies
- d) Prevents evolutionary changes
Answer: d) Prevents evolutionary changes
- What factor contributes to a decrease in the percentage of heterozygous individuals without altering allele frequency?
- a) Genetic drift
- b) Selection
- c) Non-random mating
- d) Mutation
Answer: c) Non-random mating
- What is the role of genetic drift in small populations?
- a) Enhances genetic diversity
- b) Prevents allele loss
- c) Causes random fluctuations, leading to allele loss
- d) Stabilizes gene frequencies
Answer: c) Causes random fluctuations, leading to allele loss
- What is the primary outcome of selection in a population?
- a) Decrease in genetic diversity
- b) Increase in random mating
- c) Stabilization of allele frequencies
- d) Differential reproductive success
Answer: d) Differential reproductive success
- In the Hardy-Weinberg equation (P2 + 2Pq + q2 = 1), what does 2Pq represent?
- a) Homozygous allele frequency
- b) Recessive allele frequency
- c) Heterozygous allele frequency
- d) Dominant allele frequency
Answer: c) Heterozygous allele frequency
- What is the frequency of a fixed allele in the gene pool?
- a) 0.5
- b) 0.75
- c) 1.0
- d) 0.0
Answer: c) 1.0
- How does inbreeding influence allele frequency in a population?
- a) Increases heterozygosity
- b) Causes random fluctuations
- c) Decreases genetic diversity
- d) Stabilizes gene frequencies
Answer: c) Decreases genetic diversity
- What is the role of mutations in changing allele frequency in a population?
- a) Common mutations significantly alter allele frequency
- b) Rare mutations have minimal impact on allele frequency
- c) Mutations always lead to allele fixation
- d) Mutations prevent genetic drift
Answer: b) Rare mutations have minimal impact on allele frequency
- What does the Hardy-Weinberg theorem state about the effect of meiosis and random fertilization on the overall genetic structure of a population?
- a) They lead to allele fixation
- b) They cause random fluctuations in allele frequencies
- c) They have no effect on the overall genetic structure
- d) They stabilize gene frequencies
Answer: c) They have no effect on the overall genetic structure
Frequently Asked Questions (FAQs):
1. What is the Hardy-Weinberg theorem?
- Answer: The Hardy-Weinberg theorem is an algebraic formula that describes hereditary equilibrium within a population. It states that the frequencies of alleles and genotypes in a population’s gene pool remain constant over generations unless acted upon by factors other than sexual recombination.
2. Who were the scientists behind the Hardy-Weinberg theorem?
- Answer: The theorem is named after Wilhelm Weinberg, a German physician, and Godfrey Harold Hardy, a British mathematician, who independently derived the principle in 1908.
3. What is a gene pool?
- Answer: The gene pool is the total aggregate of genes in a population at any one time. It includes all alleles at all gene loci in all individuals of the population.
4. How is allele frequency represented in the Hardy-Weinberg equation?
- Answer: In the Hardy-Weinberg equation, population geneticists use the letter P to represent the frequency of the dominant allele and the letter q to represent the frequency of the recessive allele.
5. What happens if all members of a population are homozygous for the same allele?
- Answer: If all members are homozygous for the same allele, that allele is considered fixed in the gene pool.
6. How is genetic diversity maintained in a population according to the Hardy-Weinberg theorem?
- Answer: The theorem states that the frequencies of alleles and genotypes remain constant over generations unless acted upon by factors other than sexual recombination, maintaining genetic diversity.
7. What is the role of mutations in changing allele frequency?
- Answer: Mutations are the ultimate source of modifications, but individual mutations occur so rarely that mutation alone does not significantly change allele frequency.
8. How does migration affect gene frequency?
- Answer: Migration acts to prevent evolutionary changes by avoiding divergence between populations. Emigration and migration disrupt the gene pool.
9. What is genetic drift, and how does it affect small populations?
- Answer: Genetic drift is the change in frequency of alleles by chance. In small populations, fluctuations due to genetic drift may lead to the loss of particular alleles.
10. How does non-random mating influence allele frequency?
- Answer: Non-random mating, especially inbreeding, reduces the percentage of heterozygous individuals without altering allele frequency.
11. What is the role of selection in changing gene frequencies in a population?
- Answer: Selection, whether artificial or natural, influences the proportions of genes in a population by favoring individuals with specific traits, leading to changes in gene frequencies.
12. How is the Hardy-Weinberg theorem related to meiosis and random fertilization?
- Answer: The theorem states that meiosis and random fertilization have no effect on the overall genetic structure of a population, as their shuffling of alleles does not impact the gene frequencies.
Summary:
In conclusion, the Hardy-Weinberg theorem provides a valuable framework for understanding the hereditary equilibrium within a population. Named after Wilhelm Weinberg and Godfrey Harold Hardy, this theorem, derived in 1908, describes the constancy of allele and genotype frequencies in a population’s gene pool over generations.
The tutorial covers key concepts such as population, gene pool, and allele frequencies. A population, defined as a localized group of individuals belonging to the same species, exhibits concentrated gene pools, shaping genetic relationships among individuals. The total aggregate of genes at any given time defines the population’s gene pool, reflecting the diversity of alleles at gene loci.
Illustrated through a vivid example of a wildflower population with distinct flower color alleles, the tutorial explores how allele frequencies translate into genotype frequencies. The Hardy-Weinberg theorem, encapsulated in a general equation, emphasizes the stability of genetic structures over generations, unaffected by meiosis and random fertilization.
Estimating allelic and genotypic frequencies using P and q for a two-allele population, the tutorial underscores the relationship between these frequencies and the overall genetic makeup of a population. The binomial expansion of the Hardy-Weinberg theorem further reinforces the theorem’s predictive power.
The tutorial concludes by examining factors that can affect gene frequency. Mutations, migration, genetic drift, non-random mating, and selection are explored as dynamic forces capable of introducing variations in gene frequencies within populations.
Understanding these principles not only enhances knowledge of population genetics but also provides insights into the mechanisms that shape genetic diversity and evolutionary trajectories in natural populations.