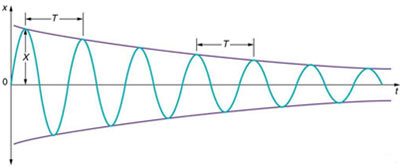
Thus, simple harmonic motion is an idealization. In practice, the amplitude of this motion gradually lessens and is smaller sized because of friction and air resistance because the energy of the oscillator is consumed in doing work against the resistive forces. The amplitude of a damped simple harmonic wave changes with time as compared to an ideal un-damped harmonic wave. Thus, we see that
Damping is the process where energy is dissipated from the oscillating system.
An application of damped oscillations is the shock absorber of an automobile which provides a damping force to prevent excessive oscillations.
Resonance
Related to the motion of a driven harmonic oscillator, there is a really striking phenomenon, called resonance. It arises if the external driving force is periodic with a duration comparable to the natural duration of the oscillator. In a resonance situation, the driving force may be feeble, and the amplitude of the motion may end up being additional normally big. When it comes to the oscillating basic pendulum, if we blow to press the pendulum whenever it can be found in front of our mouth, it is discovered that the amplitude gradually increases.
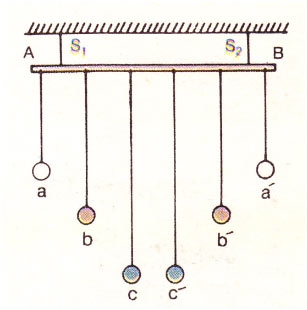
To show this resonance effect, a device is shown. A horizontal rod AB is supported by two strings S1 and S2. Three pairs of pendulums aa’, bb’ and cc’
are suspended to this rod. The length of each pair is the same but is various for different pairs. If among these pendulums, say c, is displaced in a direction perpendicular to the plane of the paper, then its resultant oscillatory movement triggers in rod AB a very small disturbing motion, whose period is the same as that of c’. Due to this small motion of the rod, each of the remaining pendulums (aa’, bb’. and qc’) undergo a minor regular motion.
This causes the pendulum c’, whose length and, hence, the duration is exactly like that of c, to oscillate backward and forward with gradually increasing amplitude. Nevertheless, the amplitudes of the other pendulums remain small throughout the subsequent movements of c and c’, because their natural periods are not the same as that of the disturbing force due to rod AB.
The energy of the oscillation originates from the driving source. At resonance, the transfer of energy is optimum. Thus, resonance takes place when the frequency of the applied periodic force is equal to one of the natural frequencies of vibration of the forced or driven harmonic oscillator.
Advantages and Disadvantages of Resonance
We stumble upon numerous examples of resonance in everyday life. A swing is a fine example of mechanical resonance. It is like a pendulum with a single natural frequency depending on its length. If a series of regular pushes are offered to the swing, its movement can be built up tremendously. If pushes are given irregularly, the swing will hardly vibrate.
The column of soldiers, while progressing a bridge of long period is recommended to break their actions. Their rhythmic march may establish oscillations of precariously large amplitude in the bridge structure.

Tuning a radio is the best example of electrical resonance. When we turn the knob of a radio, to tune a station, we are altering the natural frequency of the electric circuit of the receiver, to make it equal to the transmission frequency of the radio station. When the two frequencies match, energy absorption is maximum and this is the only station we hear.
Another fine example of resonance is the heating and cooking of food really effectively and uniformly by a microwave oven. The waves produced in this type of oven have a wavelength of 12 cm at a frequency of 2450 MHz. At this frequency, the waves are taken in due to resonance by water and fat molecules in the food, heating them up and so cooking the food.
Sharpness of Resonance
We have seen that at resonance, the amplitude of the oscillator ends up being huge. If the amplitude reduces rapidly at a frequency slightly different from the resonant frequency, the resonance will be sharp. The amplitude in addition to its sharpness, both rely on the damping. The smaller the damping, the greater the amplitude and the sharper will be the resonance.
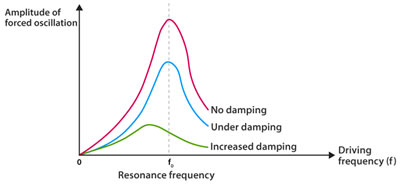
A greatly damped system has a relatively flat resonance curve.
The result of damping can be observed by connecting a pendulum having light mass such as a pith ball as its bob and another of the exact same length carrying a heavy mass such as a lead bob of equivalent size, to a rod. They are set into vibrations by the 3rd pendulum of equivalent length, attached to the very same rod. It is observed that the amplitude of the lead bob is much greater than that of the pith-ball. The damping effect for the pith-ball due to air resistance is much greater than for the lead bob.
MCQs:
- 1. Which term describes oscillations where the amplitude decreases gradually with time?
- A) Resonance
- B) Damping
- C) Sharpness
- D) Frequency
- Answer: B) Damping
- 2. What is the process by which energy is dissipated from an oscillating system?
- A) Resonance
- B) Damping
- C) Harmonization
- D) Amplification
- Answer: B) Damping
- 3. Which application is mentioned as an example of damped oscillations?
- A) Swing
- B) Radio tuning
- C) Shock absorber of an automobile
- D) Microwave oven
- Answer: C) Shock absorber of an automobile
- 4. Resonance occurs when the external driving force is periodic with a duration comparable to what?
- A) Natural duration of the oscillator
- B) Time period of the oscillator
- C) Damping ratio
- D) Amplitude of the oscillator
- Answer: A) Natural duration of the oscillator
- 5. What happens to the amplitude of motion in a resonance situation?
- A) It decreases gradually
- B) It remains constant
- C) It becomes increasingly large
- D) It becomes unpredictable
- Answer: C) It becomes increasingly large
- 6. In the example with the swing, what type of resonance is demonstrated?
- A) Mechanical resonance
- B) Electrical resonance
- C) Microwave resonance
- D) Harmonic resonance
- Answer: A) Mechanical resonance
- 7. What is the analogy used to explain resonance in tuning a radio?
- A) Swing
- B) Bridge
- C) Soldiers
- D) Microwave oven
- Answer: B) Bridge
- 8. What phenomenon occurs when the frequency of an applied force matches one of the natural frequencies of a harmonic oscillator?
- A) Resonance
- B) Damping
- C) Oscillation
- D) Harmonization
- Answer: A) Resonance
- 9. How is the sharpness of resonance affected by damping?
- A) It increases with damping
- B) It decreases with damping
- C) It remains constant
- D) It is unrelated to damping
- Answer: B) It decreases with damping
- 10. Which type of resonance results in a relatively flat resonance curve?
- A) Mechanical resonance
- B) Electrical resonance
- C) Highly damped resonance
- D) Harmonic resonance
- Answer: C) Highly damped resonance
- 11. What is the key factor determining the amplitude and sharpness of resonance?
- A) Frequency
- B) Damping
- C) Amplitude
- D) Energy
- Answer: B) Damping
- 12. What is observed when comparing the amplitude of vibrations between a pith ball and a lead bob in the example provided?
- A) Lead bob has lower amplitude
- B) Pith ball has lower amplitude
- C) Both have equal amplitudes
- D) Amplitude cannot be compared
- Answer: A) Lead bob has lower amplitude
- 13. Which factor determines the amplitude and sharpness of resonance?
- A) Length of the pendulum
- B) Mass of the bob
- C) Damping
- D) Period of oscillation
- Answer: C) Damping
- 14. What happens to the amplitude of the oscillator at resonance?
- A) It becomes maximum
- B) It remains constant
- C) It decreases
- D) It becomes unpredictable
- Answer: A) It becomes maximum
- 15. Which example demonstrates electrical resonance?
- A) Swing
- B) Radio tuning
- C) Microwave oven
- D) Soldiers marching
- Answer: B) Radio tuning
- 16. What phenomenon allows the heating and cooking of food effectively in a microwave oven?
- A) Mechanical resonance
- B) Electrical resonance
- C) Harmonic resonance
- D) Damped oscillations
- Answer: B) Electrical resonance
- 17. Which component prevents excessive oscillations in an automobile?
- A) Swing
- B) Shock absorber
- C) Radio receiver
- D) Bridge
- Answer: B) Shock absorber
Summary
In this comprehensive tutorial, we’ve dived into the damped oscillations, resonance, and the sharpness of resonance. We began by understanding damped oscillations, where the gradual reduction in amplitude over time is attributed to energy dissipation from the oscillating system, as commonly observed in phenomena such as the movement of a basic pendulum and exemplified in practical applications like shock absorbers in automobiles.
Next, we explored resonance, a phenomenon that occurs when an external driving force matches the natural frequency of a harmonic oscillator, resulting in a significant increase in amplitude. Illustrated through examples like a swing and tuning a radio, resonance showcases how energy transfer becomes optimal, making it a crucial concept in various real-world scenarios.
Additionally, we discussed the advantages and disadvantages of resonance, highlighting its diverse applications ranging from mechanical resonance in swings to electrical resonance in radio tuning and microwave ovens, where precise frequency matching maximizes energy absorption and efficiency in various processes.
Finally, we examined the sharpness of resonance, noting how damping affects both the amplitude and sharpness of resonance, with lower damping leading to higher amplitudes and sharper resonances. Through practical experiments with pendulums of varying masses, we gained insights into how damping influences resonance characteristics, emphasizing the importance of understanding damping effects in oscillatory systems.
Overall, this tutorial provides a comprehensive understanding of damped oscillations, resonance phenomena, and the nuanced dynamics of sharp resonance, offering valuable insights for both theoretical comprehension and practical applications in various fields.