Boyle’s Law
Robert Boyle was a natural philosopher, chemist, physicist, and inventor.
Boyle is considered today as the first modern chemist, and therefore one of the founders of modern chemistry, and among the pioneers of experimental scientific methods and techniques. He is best known for Boyle’s law.
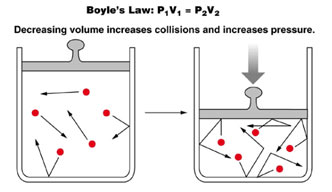
Boyle’s law is a gas law, stating that the pressure and volume of a gas have an inverse relationship.
If volume increases, then pressure decreases and vice versa, but when the temperature is held constant.
Statement
The volume of a given mass of a gas at constant temperature is inversely proportional to the pressure applied to the gas.
Mathematical Form
In Boyle’s law, the pressure and volume are variables while the temperature and quantity of a gas remains constant. So,
Vα1/P (when the temperature level and a number of moles are constant).
By putting constant
Or V= k/p
PV = k (when T and n are constant)
‘ k’ is the proportionality constant. The value of k is different for the different quantities of the same gas.
According to the equation, Boyle’s law can also be defined as
“The product of pressure and volume of a fixed quantity of a gas at constant temperature is a constant quantity”.
So,
P1V1= k, P2V2= k
Hence P1V1= P2V2
P1V1 are the initial values of pressure and volume, while P2V2 are the final values of pressure and volume.
Experimental Verification of Boyle’s Law
At a constant temperature level say at 25C, the volume of a provided amount of a gas is reduced in proportion to the increase in pressure. Let us take gas in a cylinder having a moveable piston.

The cylinder is also connected with a manometer to read the pressure of the gas. Let the initial volume of gas is 1 dm3 and its pressure is 2 atm when the piston has one weight on it. When the piston is pressed twice with the help of two equivalent weights, the pressure ends up being 4 atm.
Likewise, when the piston is filled with a mass 3 times greater, then the pressure ends up being 6 atm. The initial volume of the gas at 2 atm is1dm3 it is minimized to 1/2 dm3 and then 1/3 dm3 with an increase of weights, respectively.
P1V1 = 2 atm x 1 dm3 = 2 dm3 atm = k
P2V2 = 4 atm x 1/2 dm3 = 2 dm3 atm = k
P3V3 = 6 atm x 1/3 dm3 = 2 dm3 atm = k
For this reason, Boyle’s law is confirmed.
The value of k will stay the same for the same quantity of gas at the very same temperature.
Graphical Explanation of Boyle’s Law
Let us take a particular quantity of a gas at a constant temperature say 0C and confine it in a cylinder having a piston in it. When the pressure of the gas is different, its volume changes. An increase in pressure decreases the volume. If a graph is outlined in between pressure on the x-axis (abscissa) and volume on the y-axis (ordinate), then a curve is obtained. This curve is called isotherm ‘iso’ implies the same, “therm” implies heat. Now increase the temperature of the gas to 25 ° C.

Keep this temperature consistent and once again vary the pressure and volume, and plot the isotherm. It goes away from both the axes. The factor is that at greater temperatures, the volume of the gas has increased. Likewise, if we increase the temperature level further, make it continuous and plot another isotherm, it, even more, goes away from the axis.

If a chart is plotted between 1/V on the x-axis and the pressure P on the y-axis then a straight line is acquired. This reveals that the pressure and inverse of the volume are directly proportional to each other. This straight line will fulfill at the origin which indicates that when the pressure is really close to zero, then the volume is so high that its inverse is very near to absolutely zero.
By increasing the temperature level of the same gas from T1 to T2 and keeping it constant, one can differ pressure and volume. The graph of this information between P and 1/V will provide another straight line. This straight line at T2 will be closer to the pressure-axis.

Now, plot a graph in between pressure on the x-axis and the product PV on Y-axis. A straight line parallel to the pressure axis is obtained. This straight line suggests that ‘k’ is a constant quantity. At greater consistent temperature, the volume increase and value of product PV need to increase due to the increase of volume at same pressure, however, PV stays constant at this new temperature level and a straight line parallel to the pressure axis is acquired.
This kind of straight-line will assist us in understanding the non-ideal behaviour of gases. Boyle’s law applies just to ideal gases.

Multiple-Choice Questions (MCQs) on Boyle’s Law:
- Who is credited with the formulation of Boyle’s Law?
- A) John Dalton
- B) Robert Boyle
- C) Antoine Lavoisier
- D) Isaac Newton
Answer: B) Robert Boyle
- What does Boyle’s Law state about the relationship between pressure and volume of a gas?
- A) They have a direct relationship
- B) They have an exponential relationship
- C) They have an inverse relationship
- D) They are unrelated
Answer: C) They have an inverse relationship
- Under what condition does Boyle’s Law hold true?
- A) Constant pressure
- B) Constant temperature
- C) Constant volume
- D) Constant density
Answer: B) Constant temperature
- What does ‘k’ represent in Boyle’s Law equation?
- A) Volume
- B) Pressure
- C) Proportionality constant
- D) Temperature
Answer: C) Proportionality constant
- In Boyle’s law, if the volume of a gas increases, what happens to the pressure?
- A) Increases
- B) Decreases
- C) Remains constant
- D) Doubles
Answer: B) Decreases
- How is Boyle’s Law experimentally verified?
- A) By varying temperature and keeping the pressure constant
- B) By varying volume and keeping the temperature constant
- C) By varying pressure and keeping the volume constant
- D) By varying gas quantity and keeping the temperature constant
Answer: C) By varying pressure and keeping volume constant
- What does the graphical representation of Boyle’s Law show when pressure is plotted against volume?
- A) A curve
- B) A straight line
- C) A parabola
- D) No relationship
Answer: B) A straight line
- What happens to the graphical representation of Boyle’s Law when the temperature of the gas increases?
- A) The line shifts left
- B) The line shifts right
- C) The line becomes a curve
- D) The line remains unchanged
Answer: B) The line shifts right
- In the graphical representation of Boyle’s Law, what kind of relationship is observed between 1/V and pressure?
- A) Directly proportional
- B) Inversely proportional
- C) Exponential
- D) Unrelated
Answer: A) Directly proportional
- What is obtained when a graph is plotted between pressure and the product PV in Boyle’s Law?
- A) A curve
- B) A straight line
- C) A parabola
- D) A hyperbola
Answer: B) A straight line
- What does the straight line parallel to the pressure axis in the graph of pressure against the product PV indicate?
- A) Ideal gas behavior
- B) Non-ideal gas behavior
- C) A phase transition
- D) Constant volume
Answer: A) Ideal gas behavior
- Under what condition does Boyle’s Law apply according to the last statement?
- A) High temperature
- B) Low pressure
- C) Ideal gas
- D) Non-ideal gas
Answer: C) Ideal gas
- Who is considered one of the founders of modern chemistry and is best known for Boyle’s Law?
- A) John Dalton
- B) Robert Boyle
- C) Antoine Lavoisier
- D) Isaac Newton
Answer: B) Robert Boyle
Frequently Asked Questions (FAQs)
- Who was Robert Boyle, and why is he famous in the field of chemistry?
- Robert Boyle was a natural philosopher, chemist, physicist, and inventor. He is considered one of the founders of modern chemistry and is best known for Boyle’s Law, which describes the relationship between the pressure and volume of a gas.
- What is Boyle’s Law?
- Boyle’s Law is a gas law that states the pressure and volume of a gas have an inverse relationship when the temperature is held constant. In simple terms, as the volume of a gas increases, its pressure decreases, and vice versa.
- How is Boyle’s Law experimentally verified?
- Boyle’s Law is experimentally verified by measuring the changes in volume as the pressure of a gas is varied at constant temperature. A common experimental setup involves a cylinder with a moveable piston and a manometer to measure pressure.
- What does the statement of Boyle’s Law mean?
- The statement of Boyle’s Law is: “The volume of a given mass of a gas at constant temperature is inversely proportional to the pressure applied to the gas.” This means that if you increase the pressure on a gas, its volume will decrease, and vice versa.
- What happens to the volume of a gas when its pressure is increased, according to Boyle’s Law?
- According to Boyle’s Law, if the pressure on a gas is increased, its volume decreases. The relationship is inversely proportional.
- Explain the graphical representation of Boyle’s Law.
- The graphical representation of Boyle’s Law involves plotting a curve (isotherm) between pressure and volume. As pressure increases, volume decreases, creating a curve. Additionally, plotting 1/V against pressure results in a straight line.
- Why does the isotherm curve shift as the temperature of the gas increases?
- The isotherm curve shifts as the temperature increases because, at higher temperatures, the volume of the gas also increases. This shift is observed in graphical explanations of Boyle’s Law.
- What does the straight line parallel to the pressure axis indicate in the graph of pressure against the product PV?
- The straight line parallel to the pressure axis indicates that the product PV is a constant quantity (‘k’). This line helps us understand the non-ideal behavior of gases.
- Does Boyle’s Law apply to all gases?
- Boyle’s Law applies specifically to ideal gases. It describes the behavior of gases under conditions where the gas particles have no volume and do not interact with each other.
- What conditions are necessary for Boyle’s Law to hold true?
- Boyle’s Law holds true when the temperature is constant. If the temperature changes, the relationship between pressure and volume described by Boyle’s Law may be altered.
- How can Boyle’s Law be used to predict the behavior of gases?
- Boyle’s Law provides insights into how changes in pressure and volume affect each other when temperature is constant. This information is valuable in predicting the behavior of gases in various conditions.
- Can Boyle’s Law be applied to real gases?
- Boyle’s Law is an idealization that assumes gases behave ideally. In reality, real gases may deviate from the behavior predicted by Boyle’s Law, especially under conditions of high pressure or low temperature.
Boyle’s Law Problems/Solutions
Problem 1:
A gas has a volume of 3.0 L at a pressure of 2.5 atm. If the pressure is increased to 4.0 atm while keeping the temperature constant, what will be the new volume?
Solution 1:
Using Boyle’s Law: P1V1 = P2V2
(2.5)(3.0) = (4.0)(V2)
Solving for V2: V2 = 1.875 L
Problem 2:
A gas occupies 8.0 L at 5.0 atm. If the pressure is decreased to 3.0 atm while keeping the temperature constant, what will be its new volume?
Solution 2:
Using Boyle’s Law: P1V1 = P2V2
(5.0)(8.0) = (3.0)(V2)
Solving for V2: V2 = 13.33 L
Problem 3:
A gas has a volume of 6.0 L at 4.0 atm. If the volume is increased to 9.0 L while keeping the temperature constant, what will be the new pressure?
Solution 3:
Using Boyle’s Law: P1V1 = P2V2
(4.0)(6.0) = (P2)(9.0)
Solving for P2: P2 = 2.67 atm
Problem 4:
A gas has a volume of 10.0 L at 3.0 atm. If the volume is halved while keeping the temperature constant, what will be the new pressure?
Solution 4:
Using Boyle’s Law: P1V1 = P2V2
(3.0)(10.0) = (P2)(5.0)
Solving for P2: P2 = 6.0 atm
Problem 5:
A gas has a volume of 2.0 L at 6.0 atm. If the volume is reduced to 1.0 L while keeping the temperature constant, what will be the new pressure?
Solution 5:
Using Boyle’s Law: P1V1 = P2V2
(6.0)(2.0) = (P2)(1.0)
Solving for P2: P2 = 12.0 atm
Problem 6:
A gas occupies 5.0 L at a pressure of 3.0 atm. If the volume is tripled while keeping the temperature constant, what will be the new pressure?
Solution 6:
Using Boyle’s Law: P1V1 = P2V2
(3.0)(5.0) = (P2)(15.0)
Solving for P2: P2 = 1.0 atm
Problem 7:
A gas has a volume of 12.0 L at a pressure of 2.0 atm. If the pressure is doubled while keeping the temperature constant, what will be the new volume?
Solution 7:
Using Boyle’s Law: P1V1 = P2V2
(2.0)(12.0) = (4.0)(V2)
Solving for V2: V2 = 6.0 L
Problem 8:
A gas has a volume of 8.0 L at a pressure of 4.0 atm. If the volume is halved while keeping the temperature constant, what will be the new pressure?
Solution 8:
Using Boyle’s Law: P1V1 = P2V2
(4.0)(8.0) = (P2)(4.0)
Solving for P2: P2 = 8.0 atm
Problem 9:
A gas has a volume of 6.0 L at a pressure of 3.0 atm. If the volume is doubled while keeping the temperature constant, what will be the new pressure?
Solution 9:
Using Boyle’s Law: P1V1 = P2V2
(3.0)(6.0) = (P2)(12.0)
Solving for P2: P2 = 1.5 atm
Problem 10:
A gas occupies 10.0 L at a pressure of 5.0 atm. If the volume is reduced to 4.0 L while keeping the temperature constant, what will be the new pressure?
Solution 10:
Using Boyle’s Law: P1V1 = P2V2
(5.0)(10.0) = (P2)(4.0)
Solving for P2: P2 = 12.5 atm
Problem 11:
A gas has a volume of 15.0 L at a pressure of 2.5 atm. If the volume is increased to 20.0 L while keeping the temperature constant, what will be the new pressure?
Solution 11:
Using Boyle’s Law: P1V1 = P2V2
(2.5)(15.0) = (P2)(20.0)
Solving for P2: P2 = 1.875 atm
Problem 12:
A gas has a volume of 9.0 L at a pressure of 1.0 atm. If the volume is halved while keeping the temperature constant, what will be the new pressure?
Solution 12:
Using Boyle’s Law: P1V1 = P2V2
(1.0)(9.0) = (P2)(4.5)
Solving for P2: P2 = 2.0 atm
Problem 13:
A gas has a volume of 7.0 L at a pressure of 4.0 atm. If the pressure is reduced to 2.0 atm while keeping the temperature constant, what will be the new volume?
Solution 13:
Using Boyle’s Law: P1V1 = P2V2
(4.0)(7.0) = (2.0)(V2)
Solving for V2: V2 = 14.0 L
Problem 14:
A gas has a volume of 20.0 L at a pressure of 2.0 atm. If the volume is tripled while keeping the temperature constant, what will be the new pressure?
Solution 14:
Using Boyle’s Law: P1V1 = P2V2
(2.0)(20.0) = (P2)(60.0)
Solving for P2: P2 = 0.67 atm
Problem 15:
A gas occupies 18.0 L at a pressure of 3.0 atm. If the volume is reduced to 6.0 L while keeping the temperature constant, what will be the new pressure?
Solution 15:
Using Boyle’s Law: P1V1 = P2V2
(3.0)(18.0) = (P2)(6.0)
Solving for P2: P2 = 9.0 atm
Summarizing Boyle’s Law
Boyle’s Law, attributed to the pioneering work of Robert Boyle, stands as a fundamental principle in the realm of gas laws. This law articulates an inverse relationship between the pressure and volume of a gas when the temperature is held constant. The key components of Boyle’s Law include a statement defining the relationship between the volume and pressure of a gas, a mathematical formulation denoting the proportionality between volume and the inverse of pressure, and an experimental verification that showcases the law’s validity.
The mathematical expression, PV=k, encapsulates Boyle’s Law, where P represents pressure, V symbolizes volume, and k denotes a proportionality constant unique to each gas quantity. The law asserts that the product of pressure and volume for a fixed quantity of gas at constant temperature remains a constant value.
Experimental verification involves manipulating the volume and pressure of a gas within a cylinder, showcasing the law’s practical application. The experiments confirm that as the volume of a gas decreases, the pressure increases, validating Boyle’s Law.
Graphical explanations further elucidate Boyle’s Law by illustrating isotherms, curves that depict the relationship between pressure and volume at different temperatures. These graphs emphasize the consistent nature of the product PV, highlighting its stability despite changes in volume and pressure.
In essence, Boyle’s Law provides valuable insights into the behavior of gases, particularly ideal gases, and its foundational principles contribute significantly to the understanding of gas properties and behaviors in scientific applications.
