Bond Energy (bond enthalpy)
When a bond is formed between two atoms, energy is released. The same amount of energy is absorbed when the bond is broken to form neutral atoms. So, the bond energy is the general amount of energy needed to break all bonds of a specific type in one mole of the substance.
- It is identified experimentally, by measuring the heat involved in a chain reaction. It is also called bond enthalpy, as it is a procedure of enthalpy change at 298 K.
- The enthalpy changes in splitting a particle into its part atoms are called, enthalpy of atomization.
- The bond energy is given in kj mol-1 which is the energy required to break an Avogadro’s number (6.02 x 1023) of bonds.
- It is also released when an Avogadro’s number of bonds are formed.
- It may be noted that the energies of several bonds are greater than those of single bonds.
- But a double bond is not two times as strong as a single bond or a triple bond is not thrice as strong as a single bond.
- It suggests that s-bond is more powerful than a p-bond. Likewise, a polar covalent bond is more powerful than a non-polar covalent bond.
Ionic Character and Bond Energy
Bond energy is a measure of the strength of a bond. The strength of a bond depends on the following aspects.
- Electronegativity difference of bonded atoms
- (ii) Sizes of the atoms
- (iii) Bond length
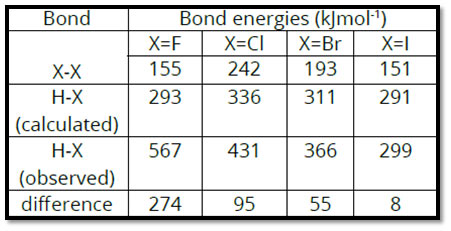
Let us think about, first, the part played by the electronegativity difference. Take a look at the bond energies of H-X type of substances, where X= F, Cl, Br, I. The table shows that electrons are not equally shared in between the bonded atoms i.e., HX. As the halogen atom is more electronegative, the bonded set is more drawn in towards the X atom and consequently, polarity is established. This triggers additional attracting force for bonding.
From the difference between speculative bond energies and those determined by presuming equivalent sharing, it is possible to approximate relative electronegativities. The comparison of these values shows that the discrepancy is the greatest for HF and the least for HI.
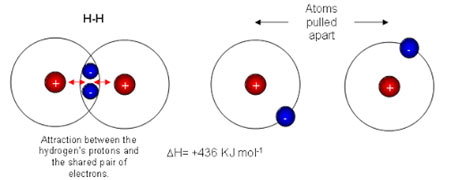
Let us determine, the increase in the strength of the H-Cl bond, due to the ionic character present in it. The H-H bond energy is 436 kJ mol-1. It indicates 436 kJ of heat is needed to break Avogadro’s number of H2 molecules into individual atoms. Hence, bond energy per bond is 72.42 x 10-23kJ.
This is obtained by dividing 436 by 6.02 x 1023. As the bonding electron set is similarly shared in between the two H atoms, we can presume that each bonded H-atom contributes half of the bond energy i.e., 36.21×10-23kJ. Similarly, the bond energy for Cl2 is 240 kJ mol-1. Therefore, each Cl-atom should contribute 19.93 x 10-23 kJ to any bond, where sharing of an electron set is equivalent.
Let us, now consider, the bond in HCl. This bond is polar; however, we think about the electron set to be similarly shared. On adding up the bond energy contributions of H-atom and Cl-atom, we anticipate the bond energy of H-Cl to be 56.14 x 10-23kJ per particle which is the sum of 36.21×10-23kJ and 19.93 x10-23kJ.
For Avogadro’s number of HCl molecules, the calculated bond energy is 337.96 kJmol-1 which is acquired by increasing 56.14 x 10 -23 with 6.02 x 10-23. The experimentally found bond energy for HCl is 431 kJmol-1. The observed bond energy is significantly greater than the computed value which means a more steady H-Cl bond. This stability is because of the ionic character present in the molecule. The decreasing polarity from HF to HI shows a pattern towards equivalent sharing of electrons which is consistent with decreasing electronegativity from F to I.
The bonds with greater bond energy values have shorter bond lengths. The bond energies of C-to-C bonds are in the order C ≡ C >C=C>C-C. Their bond lengths remain in the reverse order i.e.,C -C > C=C > C ≡ C.
Bond Length
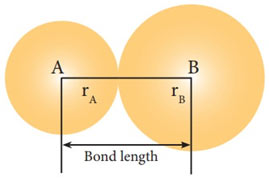
The distance between the nuclei of two atoms forming a covalent bond is called the bond length.
 between the positive and negative centers (r
between the positive and negative centers (r
The bond lengths are experimentally determined by physical methods. The techniques might be electron diffraction, X-ray diffraction, or spectral studies. The covalent bond length in between 2 atoms is frequently but not constantly independent of the nature of the particles. For instance, in the majority of the aliphatic hydrocarbons, the C-C bond length is near to 154 pm. The C-C bond length is also found to be the very same in diamonds.
The covalent radii for different elements are almost addictive in nature. The single bond covalent radius of carbon is 77 pm which is half of the C-C bond length (154 pm). Likewise, the covalent radius of Cl is 99 pm i.e., one-half of the Cl-Cl bond length (198 pm). So, the bond length of the C-Cl bond will be 77 + 99= 176 pm.
With an increase in electronegativity difference between the bonded atoms, the bond ends up being shortened. For example, Si-F bond length in SiF4 is found to be 154-159 pm, whereas the addition of their covalent radii (Si= 117 pm and F= 64 pm) gives Si-F bond length to be equal to 181 pm. The calculated values are often higher due to electronegativity differences. The ionic character leads to a reduction of the bond length due to the force of attraction in between the polar ends.
Furthermore, the hybridization plan included likewise discusses the reduction of bonds due to the predominant participation of s-orbitals. Because the 2s-orbital of carbon has a smaller mean radius than the 2p-orbitals, it would be expected that the greater the s character in the hybrid orbitals utilized, the shorter the bond distance. Hence, the C-C bond lengths are 154,133 and 120 pm for ethane, ethene, and ethyne, respectively where s orbital contribution increases from sp3 to sp. Further, p-bonding likewise minimizes the internuclear bond distance. The bond length increases, as we move from top to bottom in group IV-A of the periodic table.
Hence, Si-Si bond length is more than C-C bond length in group IV-A and P-P bond length is a lot more than N-N bond length in group V-A. As the atomic radii increase in a group (N to P or C to Si), the effect of the effective nuclear charge decreases on electrons. As a result, the bond length will increase.
In the periodic table, reduction of bond lengths occurs from delegated right in, a period. This can be attributed to the pull by a nuclear charge with the same value of the principal quantum number. For that reason, C-C bond length is greater than N-N bond length.
Dipole Moment
In heteronuclear molecules, e.g., HCl where the bonded atoms are of different elements, the molecule ends up being polar due to the electronegativity difference. Partial positive and negative charges become separated on the bonded atoms. The separation of these charges on the particle is called a dipole and the molecule is stated to have a dipole moment. The dipole moment is a vector quantity, which has a magnitude along with a direction.
” The dipole moment (m) is defined as the product of the electric charge (q) and the distance between the positive and negative centers (r):”
µ= q x r
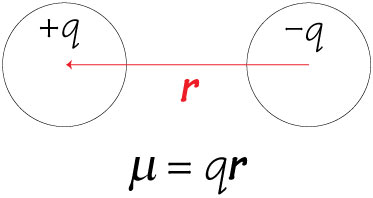
The dipole moments of simple heteronuclear diatomic molecules like HF, HCl, HBr. HI, CO, NO, and so on are directed from electropositive ends to electronegative ends.
The dipole moments are determined in Debye (D) systems. Let us think about a theoretical molecule (A *– B-), or a unit negative charge separated from a unit positive charge by distance r = 100 pm (1 Å) The dipole moment of such a molecule can be calculated by increasing the distance 100pm to charge of one electron or proton is 1.6 orx10-19C m= (1.6022×10-19C) x(100×10-12m) = 1.6022×10-29 mC.
Another unit of dipole moment is Debye. The equivalence of Debye and mC is 1 D = 3.336×10-30mC. So, the dipole moment of the, above system in Debye units is
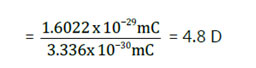
Dipole moment provides two kinds of information about the molecular structure:
- (i) Percentage ionic character of a bond
- (ii) Angles between the bonds or the geometry of molecules
(1) Percentage ionic character of a bond
From the experimentally identified dipole moments, the percentage ionic character in a bond can be calculated. For this function, we ought to understand the real dipole moments of the particle and real bond, length. The dipole moment of 100% ionic compound is represented as µionic.
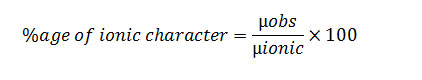
(2) Bond Angles or the Geometry of Molecules
We can understand this element by taking some important examples.
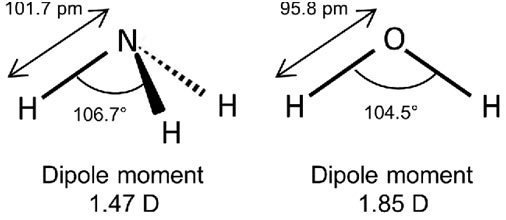
The dipole moment of water is 1.85 D which eliminated its linear structure. The estimations reveal that water has an angular structure with a bond angle of 104.5 ° in between the two O-H bonds. A linear water particle (H-O-H) would have absolutely no dipole moment. Similarly, the triatomic particles H2S or SO2 and so on are also bent like H2O.CO has a dipole moment while CO2 does not have any.
The factor is that CO2 has a linear structure, where the dipoles being equivalent and opposite, counteract each other’s effect. Likewise, CS2 has no dipole moment. Symmetrical triangular planar molecules of BF3, AlCl3, and completely tetrahedral particles like CH4, SiH4, CCl4 also have absolutely no dipole moments. This is all due to the cancellation of individual bond moments.
Multiple Choice Questions (MCQs) with Answers
- What is bond energy?
- a) Energy released when a bond is formed
- b) Energy needed to break a bond
- c) Both a and b
- d) None of the above
- Answer: c
- How is bond energy experimentally identified?
- a) By measuring the heat involved in a chain reaction
- b) By analyzing bond lengths
- c) By counting the number of bonds
- d) By observing color changes
- Answer: a
- Which factor does NOT affect bond strength?
- a) Electronegativity difference
- b) Sizes of the atoms
- c) Bond length
- d) Molecular weight
- Answer: d
- What is the unit of bond energy?
- a) Joules per mole
- b) Kilograms per mole
- c) Watts per mole
- d) Hertz per mole
- Answer: a
- How does the bond length change with an increase in electronegativity difference between bonded atoms?
- a) It decreases
- b) It increases
- c) It remains constant
- d) It becomes zero
- Answer: a
- What is the bond length?
- a) Distance between the nuclei of two atoms forming a covalent bond
- b) Length of a single bond
- c) Distance between two molecules
- d) Width of a bond
- Answer: a
- Why do bonds with higher bond energy values have shorter bond lengths?
- a) Due to the size of the atoms
- b) Due to increased polarity
- c) Due to attractive forces
- d) Due to decreased electronegativity
- Answer: c
- What factor explains the reduction of bond lengths in molecules with higher s-character?
- a) Hybridization
- b) Electronegativity
- c) Molecular weight
- d) Magnetic properties
- Answer: a
- In heteronuclear molecules, what is the result of electronegativity difference between bonded atoms?
- a) Longer bond length
- b) Shorter bond length
- c) Non-polarity
- d) Ionic character
- Answer: d
- What is the dipole moment?
- a) Magnitude of the charge
- b) Separation of charges in a molecule
- c) Length of a bond
- d) Molecular weight
- Answer: b
- How is the dipole moment measured?
- a) In Coulombs
- b) In Amps
- c) In Debye units
- d) In Farads
- Answer: c
- What information does the dipole moment provide about the molecular structure?
- a) Molecular weight
- b) Bond length
- c) Percentage ionic character
- d) Molecular geometry
- Answer: d
- Which molecule has a linear structure and zero dipole moment?
- a) H2O
- b) CO2
- c) CH4
- d) HCl
- Answer: b
- What is the unit of dipole moment?
- a) Coulomb per meter
- b) Debye
- c) Hertz
- d) Joule
- Answer: b
- In which molecule do symmetrical triangular planar and tetrahedral structures result in zero dipole moment?
- a) H2O
- b) CO2
- c) BF3
- d) HCl
- Answer: c
Frequently Asked Questions (FAQs):
1. What is bond energy, and how is it determined?
- Bond energy, or bond enthalpy, is the amount of energy required to break all bonds of a specific type in one mole of a substance. It is experimentally identified by measuring the heat involved in a chain reaction.
2. How is bond energy related to bond formation and breaking?
- When a bond is formed between two atoms, energy is released, and the same amount of energy is absorbed when the bond is broken to form neutral atoms.
3. What factors affect the strength of a bond?
- The strength of a bond depends on electronegativity difference between bonded atoms, sizes of the atoms, and bond length.
4. Why are the energies of multiple bonds not simply multiples of single bonds?
- A double bond is not twice as strong as a single bond, and a triple bond is not thrice as strong. This suggests that s-bonds are more powerful than p-bonds, and polar covalent bonds are stronger than non-polar covalent bonds.
5. How does electronegativity difference influence bond energy?
- Electronegativity difference results in uneven sharing of electrons, creating polarity in the bond and additional attracting forces.
6. Why is the H-Cl bond energy higher than calculated, indicating stability?
- The H-Cl bond energy is higher due to the ionic character present, making the bond more stable than expected.
7. How are bond lengths determined?
- Bond lengths are experimentally determined by physical methods such as electron diffraction, X-ray diffraction, or spectral studies.
8. How does electronegativity difference affect bond length?
- An increase in electronegativity difference shortens the bond length, and ionic character further reduces the bond length due to attractive forces between polar ends.
9. What role does hybridization play in bond length?
- Hybridization, especially with higher s-character, contributes to shorter bond distances. For example, C-C bond lengths decrease from sp3 to sp hybridization.
10. How does the dipole moment provide information about molecular structure?
- The dipole moment gives insights into the percentage ionic character of a bond and angles between bonds, revealing the geometry of molecules.
11. How is the dipole moment measured, and what is its unit?
- The dipole moment is measured in Debye units (D), and it is calculated as the product of the electric charge and the distance between positive and negative centers.
12. What does a dipole moment reveal about molecular geometry?
- It provides information about bond angles and the overall geometry of molecules. For example, non-linear structures like H2O have nonzero dipole moments.
13. Why do some molecules have zero dipole moments?
- Symmetrical molecules, such as BF3 and completely tetrahedral structures like CH4, have zero dipole moments due to the cancellation of individual bond moments.
14. How does the dipole moment help determine percentage ionic character?
- The experimentally identified dipole moments can be used to calculate the percentage ionic character in a bond, providing insights into the nature of the bond.
15. Which molecules have non-zero dipole moments and why?
- Molecules with uneven distribution of electronegativity, like HCl or CO, have non-zero dipole moments as partial charges become separated on bonded atoms.
Tutorial Summary: Bond Energy, Bond Length, and Dipole Moment
This tutorial explores the fundamental concepts of bond energy, bond length, and dipole moment, providing a comprehensive understanding of molecular interactions.
1. Bond Energy (Bond Enthalpy):
- Bond energy is the energy required to break all bonds of a specific type in one mole of a substance.
- Determined experimentally by measuring heat in a chain reaction.
- Also known as bond enthalpy, indicating enthalpy change at 298 K.
- Bond energy is given in kJ mol⁻¹, representing the energy required to break Avogadro’s number of bonds.
2. Ionic Character and Bond Energy:
- Bond energy is influenced by electronegativity difference, atom sizes, and bond length.
- Electronegativity difference leads to uneven electron sharing, creating polarity and additional bonding forces.
- Examines the increase in H-Cl bond strength due to ionic character, showing a more stable bond than calculated.
3. Bond Length:
- The distance between nuclei in a covalent bond is termed bond length.
- Experimentally determined using methods like electron diffraction and X-ray diffraction.
- Bond lengths depend on electronegativity difference, atomic radii, and hybridization.
- Greater electronegativity difference shortens the bond length, while hybridization and ionic character further influence it.
4. Dipole Moment:
- Heteronuclear molecules, like HCl, exhibit polarity due to electronegativity differences.
- Dipole moment (µ) is a vector quantity, representing the separation of positive and negative charges.
- µ = q × r, where q is electric charge and r is the distance between charges.
- Dipole moments provide insights into percentage ionic character and molecular geometry.
5. Additional Insights:
- Examines dipole moments in Debye units and their equivalence to mC.
- Discusses how dipole moments reveal percentage ionic character in bonds.
- Explains how molecular geometry influences dipole moments, using examples like water, CO, and symmetrical molecules.
In Conclusion: This tutorial equips learners with a solid foundation in understanding the energetics of bonds, their lengths, and the polarity of molecules. The interplay of these factors is crucial in unraveling the complex nature of molecular structures and behaviors.