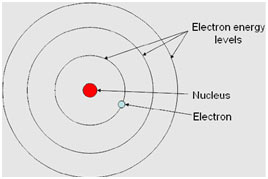
Postulate 1: Stationary State Postulate
An electron, bound to the nucleus in an atom can move around the nucleus in certain circular orbits without radiating. These orbits are called the discrete stationary states of the atom.
Postulate 2: Quantization of Angular momentum
Only those stationary orbits are allowed for which the orbital angular momentum is equal to an integral multiple of:
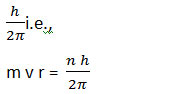
here n = 1, 2, 3, so on
n is called the principal quantum number, m and v are the mass and velocity of orbiting electron respectively and h in the equation is Plank’s constant.
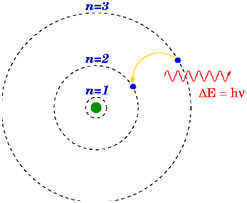
Postulate 3: Quantization of Energy
Whenever an electron makes a transition that is, jumps from high energy state E n to low energy state Ep, a photon of energy h f is emitted so that
![]()
de Broglie’s Interpretation of Bohr’s orbit
For this purpose, let suppose the string of length ‘l’. If stationary waves are set up in a stretched string. Then we can write

This is the second postulate of Bohr’s model of the hydrogen atom which was proved by de Broglie’s equation.
MCQs about Bohr’s Model of Hydrogen Atom
- 1. What did Bohr propose in 1913 regarding the atomic model of hydrogen atoms?
- A) He proposed the theory of relativity
- B) He proposed the atomic model for hydrogen atoms
- C) He proposed the theory of quantum mechanics
- D) He proposed the theory of special relativity
- Answer: B) He proposed the atomic model for hydrogen atoms
- 2. According to Bohr’s model, in which orbits can an electron move without radiating?
- A) Elliptical orbits
- B) Hyperbolic orbits
- C) Circular orbits
- D) Spiral orbits
- Answer: C) Circular orbits
- 3. What is the principal quantum number denoted by in Bohr’s model of the hydrogen atom?
- A) p
- B) n
- C) m
- D) v
- Answer: B) n
- 4. What does the quantization of angular momentum postulate in Bohr’s model state?
- A) Only certain circular orbits are allowed for the electron
- B) The angular momentum of the electron is continuous
- C) The electron moves in a random fashion around the nucleus
- D) The electron emits radiation continuously
- Answer: A) Only certain circular orbits are allowed for the electron
- 5. What is the significance of the principal quantum number � in Bohr’s model?
- A) It represents the speed of the electron
- B) It represents the mass of the electron
- C) It represents the size of the orbit
- D) It represents the charge of the nucleus
- Answer: C) It represents the size of the orbit
- 6. What does Bohr’s third postulate regarding quantization of energy state?
- A) Electrons can have any energy level
- B) Energy is continuously emitted by the electron
- C) Energy levels of the electron are discrete
- D) Energy levels of the electron are infinite
- Answer: C) Energy levels of the electron are discrete
- 7. Which scientist provided an interpretation of Bohr’s orbits using stationary waves?
- A) Albert Einstein
- B) Max Planck
- C) Louis de Broglie
- D) Niels Bohr
- Answer: C) Louis de Broglie
- 8. What property of the electron’s motion does the quantization of angular momentum explain in Bohr’s model?
- A) Its speed
- B) Its acceleration
- C) Its direction
- D) Its orbital shape
- Answer: D) Its orbital shape
- 9. Which of Bohr’s postulates explains why the electron does not spiral into the nucleus?
- A) Stationary State Postulate
- B) Quantization of Angular momentum
- C) Quantization of Energy
- D) de Broglie’s Interpretation
- Answer: A) Stationary State Postulate
- 10. What does the term “stationary states” refer to in Bohr’s model?
- A) States where the electron is not moving
- B) States where the electron’s velocity is constant
- C) States where the electron’s orbit is stable
- D) States where the electron’s energy is constant
- Answer: D) States where the electron’s energy is constant
- 11. How did Bohr combine classical and quantum physics in his model of the hydrogen atom?
- A) By using classical mechanics for the nucleus and quantum mechanics for the electron
- B) By using quantum mechanics for both the nucleus and electron
- C) By using classical mechanics for both the nucleus and electron
- D) By using relativity for both the nucleus and electron
- Answer: A) By using classical mechanics for the nucleus and quantum mechanics for the electron
- 12. What does the principal quantum number � represent in Bohr’s model of the hydrogen atom?
- A) Orbital shape
- B) Angular momentum
- C) Size of the orbit
- D) Energy level
- Answer: D) Energy level
- 13. What happens when an electron transitions from a higher energy state to a lower energy state in Bohr’s model?
- A) It absorbs a photon
- B) It emits a photon
- C) It accelerates
- D) It loses mass
- Answer: B) It emits a photon
- 14. What does the quantization of angular momentum imply about the electron’s motion in Bohr’s model?
- A) It follows a spiral path
- B) It moves randomly
- C) It follows circular orbits of specific radii
- D) It moves in elliptical orbits
- Answer: C) It follows circular orbits of specific radii
- 15. Which scientist provided an interpretation of Bohr’s orbits using the concept of stationary waves?
- A) Louis de Broglie
- B) Max Planck
- C) Werner Heisenberg
- D) Erwin Schrödinger
- Answer: A) Louis de Broglie
- 16. In Bohr’s model, what is the significance of the quantization of energy?
- A) It explains the stability of the electron’s orbit
- B) It allows the electron to emit continuous radiation
- C) It ensures the electron’s velocity remains constant
- D) It causes the electron to spiral into the nucleus
- Answer: A) It explains the stability of the electron’s orbit
Summary
At the heart of Niels Bohr’s revolutionary model of the hydrogen atom lies a fusion of classical and quantum physics, proposed in 1913 to elucidate the empirical observations of Rydberg. Bohr’s semi-classical theory was anchored on several fundamental postulates, each shedding light on the behavior of electrons within the atom.
The first postulate, the Stationary State Postulate, posits that electrons orbit the nucleus in specific, discrete circular orbits without radiating energy. These stable orbits, termed stationary states, form the foundation of Bohr’s model, providing a framework for understanding atomic structure.
Building upon this, the second postulate, the Quantization of Angular Momentum, dictates that only certain orbits are permitted, where the orbital angular momentum is quantized as an integral multiple of Planck’s constant divided by , denoted by the principal quantum number .
Linked closely is the third postulate, the Quantization of Energy, which stipulates that when electrons transition between energy levels, they emit or absorb photons with energies corresponding to the difference in energy levels. This concept explains the discrete spectral lines observed in atomic spectra.
Louis de Broglie’s interpretation of Bohr’s orbits further reinforced the model’s validity, demonstrating that the electron’s behavior could be likened to stationary waves, thereby supporting Bohr’s assertions regarding quantized orbits.
In summary, Bohr’s model of the hydrogen atom offers a remarkable synthesis of classical and quantum principles, providing profound insights into the structure and behavior of atoms, and laying the groundwork for further advancements in atomic theory and quantum mechanics.