A quick review of negative numbers
Negative numbers are expressed with a negative sign. For example, -4 is four less than zero.
When you deduct a negative number, you move to the left of the number line, due to the fact that it’s the same as adding a positive number. If you’re adding a negative number you move to the right because it’s the same as deducting a positive number.
Example
-6 + 2 = -4 6 - (-2) = 8
When you multiply a negative number by a positive number (or vice versa), the solution will be negative. If you multiply 2 negative numbers or two positive numbers, the outcome will be positive.
Example
(-6) (2) = -12 (-6) (-2) = 12
Multiplying multiple signs will generally provide you a negative solution, and multiplying the same signs will provide you a positive solution. Always suppose the number is positive if there’s no sign in front of it.
What do negative exponents mean?
There are a few various ways of thinking about negative exponents, but in general, negative exponents are the opposite of positive ones.
All negative exponents can be shown as their positive reciprocal. A reciprocal is a fraction where the numerator and denominator switch places.
Negative exponents can be expressed as the positive reciprocal of the base multiplied by on its own x times.
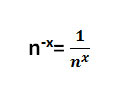
The larger the negative exponent, the smaller the number it represents. While positive exponents show repeated multiplication, negative exponents represent repeated division. That’s why 2-4is significantly greater than 2-9.
Solving of Negative Exponents
Multiplication
- If the bases of values are alike then add the exponents. Remember the rules for the addition and subtraction of negative numbers.
Example
4-24-6 = 4-8
- If the bases are not same but the exponents are the same, first of all multiply the bases then leave the exponents as they are.
Example
4-65-6 = 20-6
- If there’s nothing in common (base or exponent), start solving the equation. Flip exponents into their reciprocals and then multiply.
Example
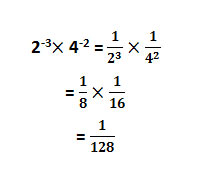
Division
- If the bases are alike then, subtract the exponents.
Remember to convert the exponent and make it positive, if required.
Example

- If the exponents are alike but the bases are different then divide the bases first.
Example

- If there is nothing in common then solve the equations.
Example

